ディジタル・フィルタで多項式の根を見つける

はじめに

意外かもしれませんが、ディジタル・フィルタを使って多項式の根を見つけることができます。

まず最初に数学的にすっきりした回路を作り、その後オーバーフローしないように改良します。

方法

$N$ 次多項式 \begin{eqnarray} F(x) &=& a_N x^N + a_{N-1}x^{N-1} + a_{N-2}x^{N-2} + \cdots + a_1 x + a_0,\ a_N\neq 0 \end{eqnarray} に対して、まず図1のような IIR 型ディジタル・フィルタの後ろに除算器をつけたものを作ります。

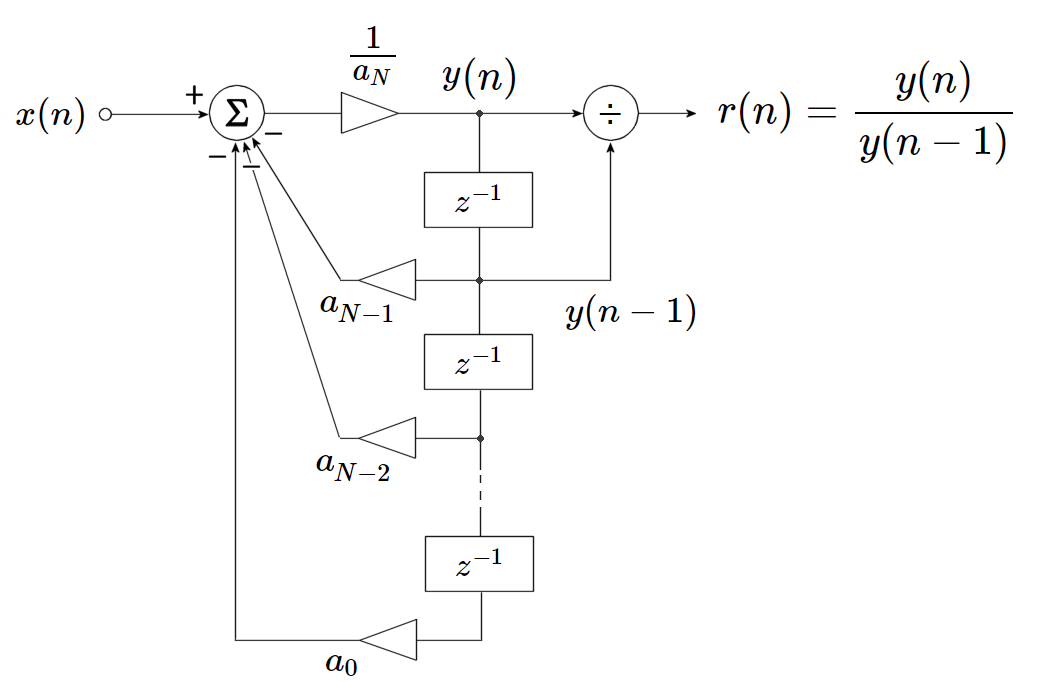
図1 : 多項式係数を持つディジタル・フィルタで絶対値最大の根を求める

このフィルタにインパルスを入力し、$y(n)$ をひとつ前の出力 $y(n-1)$ で割り算すると、出力 $r(n)$ は多項式の絶対値最大の根に収束します。

原理

本方式は代数方程式の古典的解法のひとつである Bernoulli （ ベルヌーイ ） 法に基づいていますが、ここでは信号処理的に $z$ 変換/逆変換で説明します。

図1 の除算器の左側を $z$ 領域で考えると、以下が成り立っています。 \begin{eqnarray} Y(z) &=& \frac{1}{a_N}\left(X(z)-\sum_{i=0}^{N-1} a_i z^{i-N} Y(z)\right) \\ \end{eqnarray} 変形してゆくと \begin{eqnarray} a_N Y(z) &=& X(z) - \sum_{i=0}^{N-1} a_i z^{i-N} Y(z) \\ X(z) &=& a_N Y(z) + \sum_{i=0}^{N-1} a_i z^{i-N} Y(z) \\ &=& \left(a_N + \sum_{i=0}^{N-1} a_i z^{i-N}\right) Y(z) \end{eqnarray} 両辺を $Y(z)$ で割れば、$x(n)$ から $y(n)$ への伝達関数が得られます。 \begin{eqnarray} H(z)=\frac{Y(z)}{X(z)} &=& \frac{1}{a_N + \displaystyle\sum_{i=0}^{N-1} a_i z^{i-N}} \\ &=& \frac{\displaystyle\frac{1}{a_N}}{1+\displaystyle\sum_{i=0}^{N-1} \frac{a_i}{a_N} z^{i-N}} \\ &=& \frac{\displaystyle\frac{z^N}{a_N}}{z^N + \displaystyle\sum_{i=0}^{N-1} \frac{a_i}{a_N} z^{i}} \\ &=& \frac{1}{a_N}\cdot\frac{z^N}{z^N + \displaystyle\sum_{i=0}^{N-1} \frac{a_i}{a_N} z^{i}} \end{eqnarray} 分母多項式の未知の根を $\alpha_i$ とし、それらが全て異なる非 0 の実数ならば \begin{eqnarray} z^N + \displaystyle\sum_{i=0}^{N-1} \frac{z^N}{a_N} z^{i} &=& \prod_{i=1}^N(z-\alpha_i),\\ && \alpha_i\in\mathbb{R},\\ && \alpha_i\neq \alpha_j,\ i\neq j \label{単根} \\ && \alpha_i\neq 0 \end{eqnarray} と因数分解でき、伝達関数は次のように表現できます。 \begin{eqnarray} H(z) &=& \frac{1}{a_N}\cdot\frac{z^N}{\displaystyle\prod_{i=1}^N(z-\alpha_i)} \label{Hz} \end{eqnarray}

ここで $M$ 番目の根の絶対値が唯一最大で、他に同じ絶対値を持つ根はないとしましょう。 \begin{eqnarray} |\alpha_M|\gt|\alpha_i|,\ i\neq M \end{eqnarray} 両辺を $|\alpha_M|$ で割ると、当然のことながら次式が成り立ちます。 \begin{eqnarray} \left\{ \begin{array}{ccc} \displaystyle\left|\frac{\alpha_i}{\alpha_M}\right| = 1,\ i=M \\[0.5em] \displaystyle\left|\frac{\alpha_i}{\alpha_M}\right| \lt 1,\ i\neq M \end{array} \right. \label{ratio} \end{eqnarray}

フィルタのインパルス応答 $h(n)$ は、伝達関数 $H(z)$ の逆 $z$ 変換として、次のように表せます。 \begin{eqnarray} h(n)&=& \frac{1}{2\pi i}\oint_{|\Gamma|>|\alpha_M|} H(z) z^{n-1} dz \label{oint} \end{eqnarray} 式(\ref{単根})の仮定より重根は無いので、式(\ref{oint})は次のように計算できます。 \begin{eqnarray} h(n)&=& \sum_{j=1}^N {\rm Res}_{z=\alpha_j}\left[H(z) z^{n-1}\right] \\ && 式(\ref{Hz})を代入して \nonumber\\ &=& \sum_{j=1}^N \lim_{z\to\alpha_j}(z-\alpha_j)\cdot\frac{1}{a_N}\cdot\frac{z^N}{\displaystyle\prod_{i=1}^N(z-\alpha_i)}z^{n-1} \\ &=& \frac{1}{a_N} \sum_{j=1}^N \lim_{z\to\alpha_j}\frac{z^N}{\displaystyle\prod_{i=1,\ i\neq j}^N(z-\alpha_i)}z^{n-1} \\ &=& \frac{1}{a_N} \sum_{j=1}^N \frac{\alpha_j^N}{\displaystyle\prod_{i=1,\ i\neq j}^N(\alpha_j-\alpha_i)}\alpha_j^{n-1} \end{eqnarray} これを次のように書き換えます (全ての根は非 0 の実数と仮定していますから、$\alpha_M^{n-1}$ で割っても 0 割り算は生じません)。 \begin{eqnarray} h(n) &=& \frac{\alpha_M^{n-1}}{a_N} \sum_{j=1}^N \frac{\alpha_j^N}{\displaystyle\prod_{i=1,\ i\neq j}^N(\alpha_j-\alpha_i)} \cdot \frac{\alpha_j^{n-1}}{\alpha_M^{n-1}} \end{eqnarray} さらに \begin{eqnarray} c_j &=& \frac{\alpha_j^N}{\displaystyle\prod_{i=1,\ i\neq j}^N(\alpha_j-\alpha_i)} \end{eqnarray} と置くと、インパルス応答は次式で表せることになります。 \begin{eqnarray} h(n) &=& \frac{\alpha_M^{n-1}}{a_N} \sum_{i=1}^N c_i \left(\frac{\alpha_i}{\alpha_M}\right)^{n-1} \end{eqnarray}

ディジタル・フィルタにインパルス $\delta(n)$ を入力すると、インパルス応答 $h(n)$ がそのまま出てきますから $y(n)=h(n)$ になります。 \begin{eqnarray} y(n)&=& h(n)*\delta(n) \\ &=& h(n) \\ &=& \frac{\alpha_M^{n-1}}{a_N} \sum_{i=1}^N c_i \left(\frac{\alpha_i}{\alpha_M}\right)^{n-1} \end{eqnarray}

除算器出力 $r(n)$ は $y(n)$ と $y(n-1)$ の比ですので、次のようになります。 \begin{eqnarray} \require{cancel} r(n)&=& \frac{y(n)}{y(n-1)} \\ &=& \frac{\frac{\alpha_M^{n-1}}{\cancel{a_N}}\displaystyle\sum_{i=1}^N c_i \left(\frac{\alpha_i}{\alpha_M}\right)^{n-1}}{\frac{\alpha_M^{n-2}}{\cancel{a_N}}\displaystyle\sum_{i=1}^N c_i \left(\frac{\alpha_i}{\alpha_M}\right)^{n-2}} \\ &=& \frac{\alpha_M^{\cancel{n-1}}}{\cancel{\alpha_M^{n-2}}} \cdot \frac{\displaystyle\sum_{i=1}^N c_i \left(\frac{\alpha_i}{\alpha_M}\right)^{n-1}}{\displaystyle\sum_{i=1}^N c_i \left(\frac{\alpha_i}{\alpha_M}\right)^{n-2}} \\ &=& \alpha_M \cdot \frac{\displaystyle\sum_{i=1}^N c_i \left(\frac{\alpha_i}{\alpha_M}\right)^{n-1}}{\displaystyle\sum_{i=1}^N c_i \left(\frac{\alpha_i}{\alpha_M}\right)^{n-2}} \\ \end{eqnarray} $|\alpha_M|\gt|\alpha_i|,\ i\neq M$ と仮定しましたので、式(\ref{ratio})から以下が成り立ちます。 \begin{eqnarray} \lim_{n\to\infty} \left(\frac{\alpha_i}{\alpha_M}\right)^{n-1} = \lim_{n\to\infty} \left(\frac{\alpha_i}{\alpha_M}\right)^{n-2} = \left\{ \begin{array}{c} 1, & i=M \\ 0, & i\neq M \end{array} \right. \end{eqnarray} このことより \begin{eqnarray} \lim_{n\to\infty} r(n) &=& \lim_{n\to\infty} \alpha_M \cdot \frac{\displaystyle\sum_{i=1}^N c_i \left(\frac{\alpha_i}{\alpha_M}\right)^{n-1}}{\displaystyle\sum_{i=1}^N c_i \left(\frac{\alpha_i}{\alpha_M}\right)^{n-2}} \\ && の分母子に含まれる i\neq M の項は\ 0\ になるので \nonumber\\ &=& \alpha_M \cdot \cancel{\frac{c_M}{c_M}} \\ &=& \alpha_M \end{eqnarray} よって、このフィルタにインパルス $\delta(n)$ を入力すると、出力 $r(n)$ は $n\to\infty$ で多項式 $F(x)$ の絶対値最大の根 $\alpha_M$ に収束することがわかります。

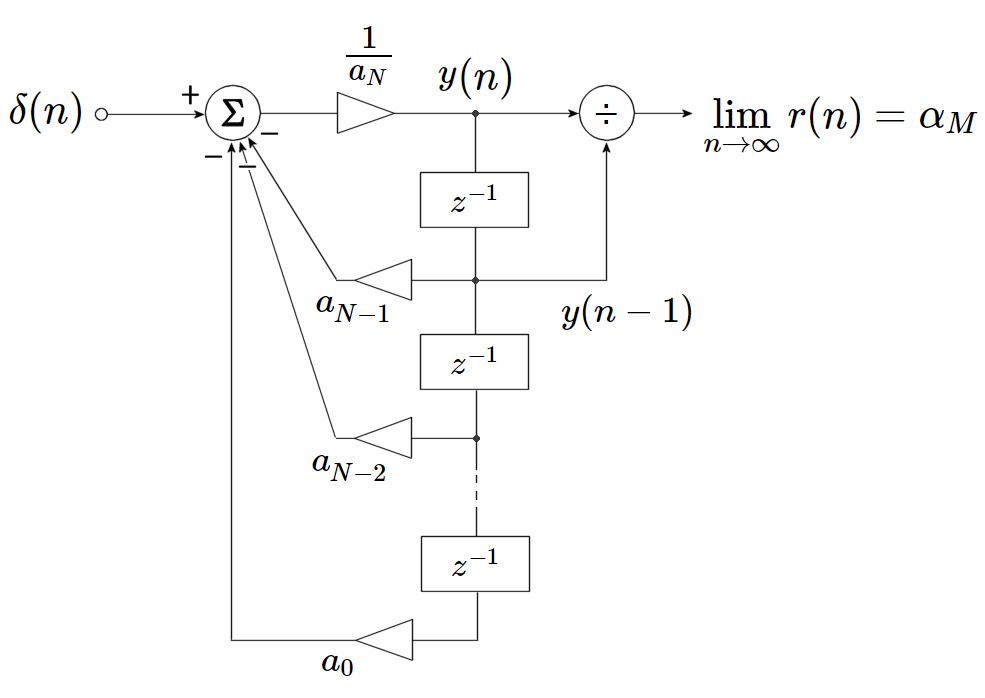
図2 : 出力 $r(n)$ は多項式の絶対値最大の根 $\alpha_M$ に収束する

計算例

例1

まず暗算でもできる簡単な問題を解いてみましょう。 \begin{eqnarray} F(x) &=& 4x-3 &=& 0 \end{eqnarray} 言うまでもなく答は $x=\displaystyle\frac{3}{4}=0.75$ です。

この場合の回路は図3のようになります。

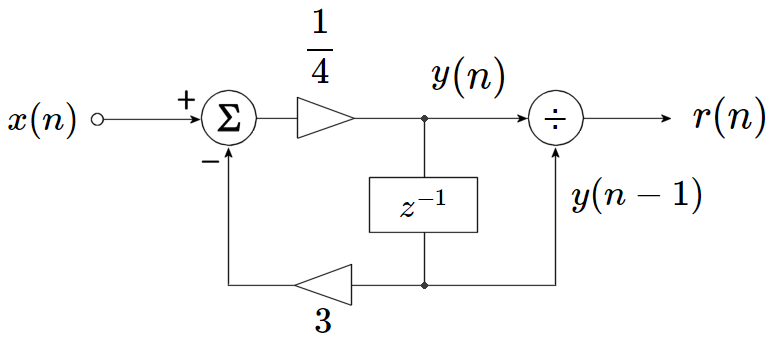
図3 : $4x-3=0$ を解く回路

インパルス $x(n)=\delta(n)$ を入力して動かしてみると、各部の値は次表のようになりました。

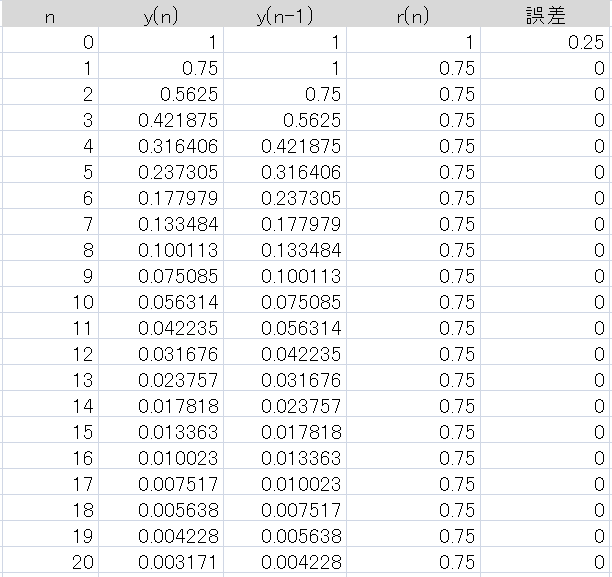
表1 : 図3の回路にインパルスを入れた時の各部の値

$n=0$ では誤差 0.25 ですが、$n=1$ では正解に到達しており、それ以降も $y(n),y(n-1)$ は変化してゆきますが、その比は一定で 0.75 を保っています。 グラフ化すると図4 のようになります。

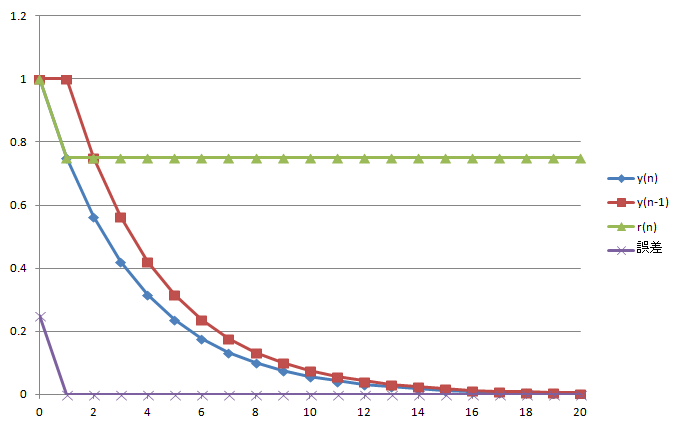
図4 : 表1 のグラフ

$n\geq 1$ では、青線と赤線の値の比が 0.75 になっています。

例2

この方法でもうひとつ、中学レベルの易しい問題を解いてみましょう。 \begin{eqnarray} F(x) &=& 3x^2-9x+6 &=& 0 \end{eqnarray}

この場合の回路は図5のようになります。

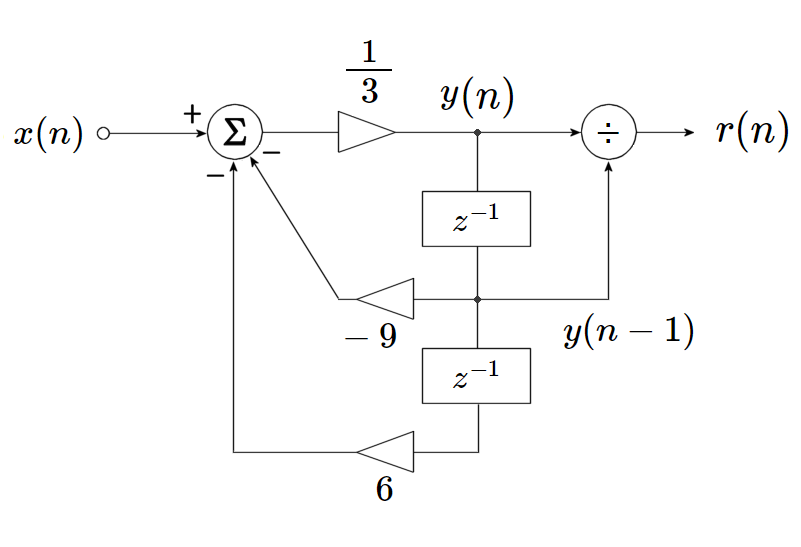
図5 : $3x^2-9x+6=0$ を解く回路

インパルス $x(n)=\delta(n)$ を入力して動かしてみると、各部の値は次表のようになりました。

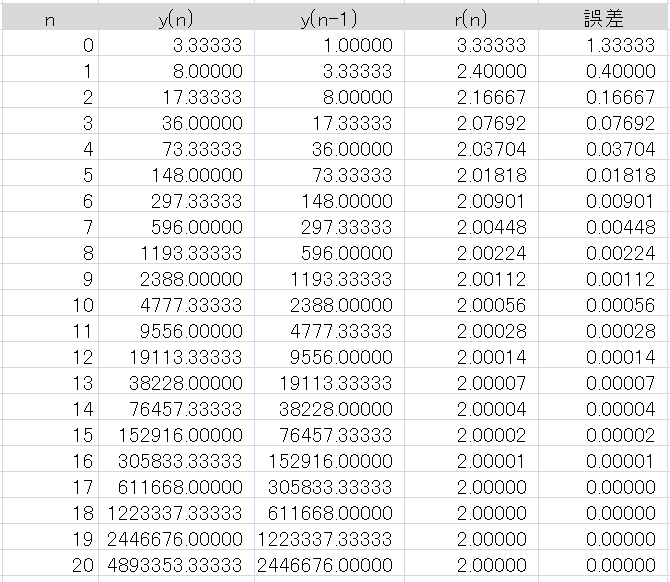
表2 : 図5の回路にインパルスを入れた時の各部の値

解かせた多項式は \begin{eqnarray} F(x) &=& 3x^2-9x+6 \\ &=& 3(x-2)(x-1) \end{eqnarray} のように因数分解され、根は 2 と 1 ですから、$r(n)$ は絶対値が大きい方の根 2 に収束しています。

数学的にはこれで「めでたし」なのですが、よく見ると $y(n), y(n-1)$ がどんどん大きくなっており、このまま放置すると、遠からずオーバーフローしてしまいそうです。

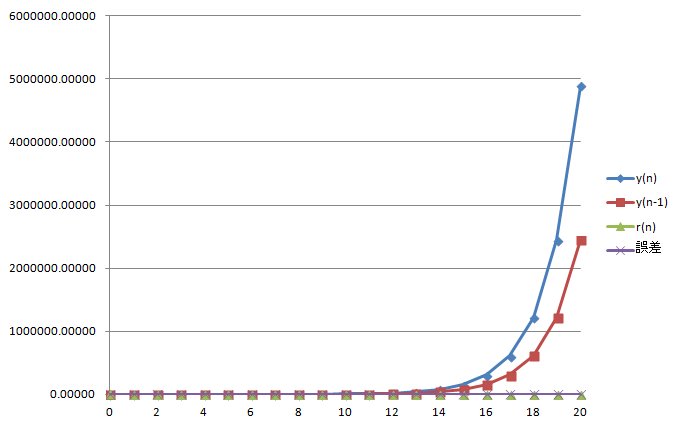
図6 : 表2 のグラフ

なぜこうなるのか考えてみましょう。出力は次のように計算されます。 \begin{eqnarray} r(n) &=& \frac{y(n)}{y(n-1)} \end{eqnarray} ということは \begin{eqnarray} y(n) &=& r(n)y(n-1) \end{eqnarray} ですから、$r(n)$ が 2 に収束する場合 (つまり絶対値最大の根が 2 なら)、反復するにつれて $y(n)$ は前回値 $y(n-1)$ の約 2 倍になってしまうわけで、コンピュータで計算するには「難アリ」です。

そこで、出力 $r(n)$ は $y(n)$ と $y(n-1)$ の相対的な比で計算され、$y(n), y(n-1)$ の絶対的な大きさには関係ないところに着目し、$r(n)$ を計算したら遅延器内容をシフトした後で全ての遅延器の値を $y(n)$ で割ることにしましょう。

その結果が表3 と図7 (数値は $r(n)$ を計算し、全遅延器を $y(n)$ で割る直前の値) です。

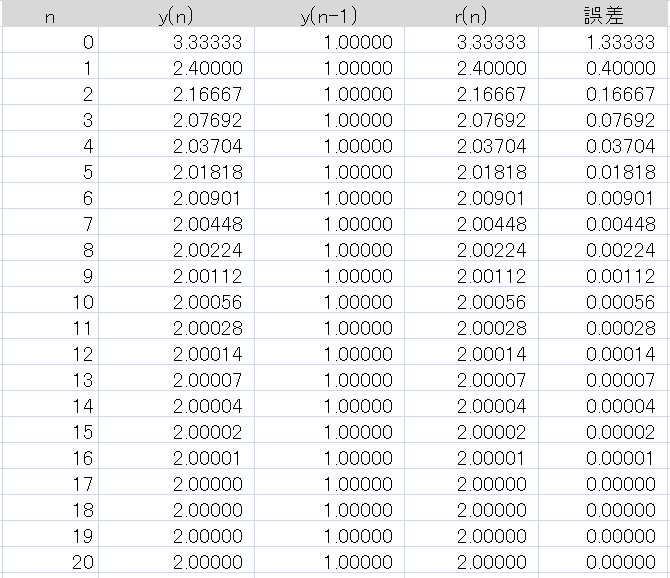
表3 : 反復毎に全遅延器の値を $r(n)$ で除算した場合

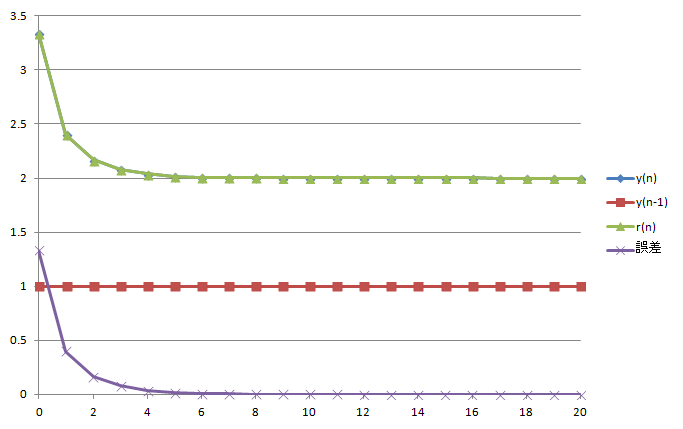
図7 : 表3 のグラフ
$y(n)$ と $r(n)$ は一致しているため、$y(n)$ の青い線は $r(n)$ の緑線の下に隠れて見えません

$y(n),\ y(n-1)$ 共に大きくならず、うまくいったようです。 しかも $y(-1)=1$ かつシフト後に全遅延器の値を $y(n)$ で割っているため、$y(n-1)$ は全て 1 になりました。 1 で割るのは無意味ですので、右側にあった除算器を取ってしまいましょう (図8)。

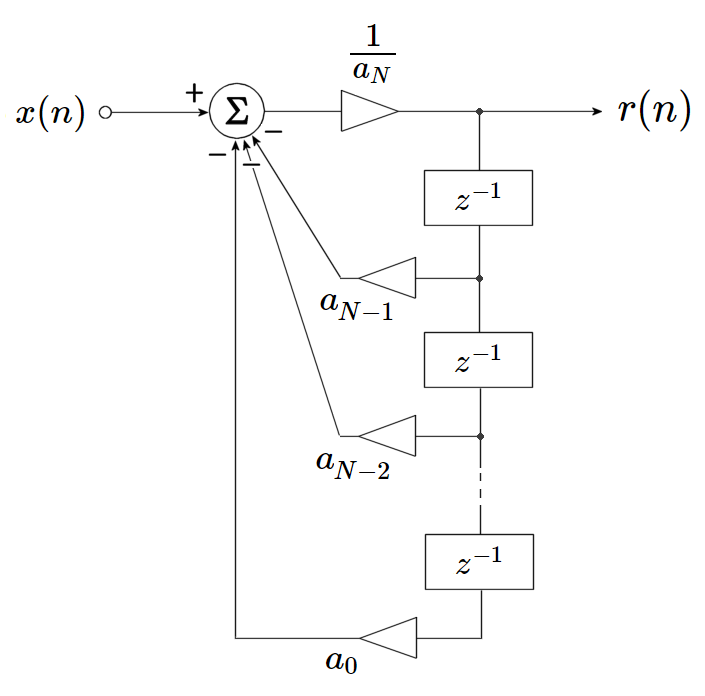
図8 : オーバーフローしない改良型

こうなると、毎回シフト後に全遅延器の内容を $r(n)$ で割ることと、一番上に $\displaystyle\frac{1}{a_N}$ の乗算器があること以外、普通の IIR です。 このフィルタのインパルス応答が係数の元になった多項式の絶対値最大根に収束するなんて、なんだか意外ですね。

例3

図8 の構成で、もう少し難しい問題を解かせてみましょう。 \begin{eqnarray} F(x) &=& x^3+6 x^2+11 x+6 &=& (x + 3) (x + 2) (x + 1) &=& 0 \end{eqnarray} 絶対値最大の根は -3 です。

この場合の回路は図9のようになります。$x^3$ の係数が 1 なので、一番上の右向きの乗算器を省略してあります。

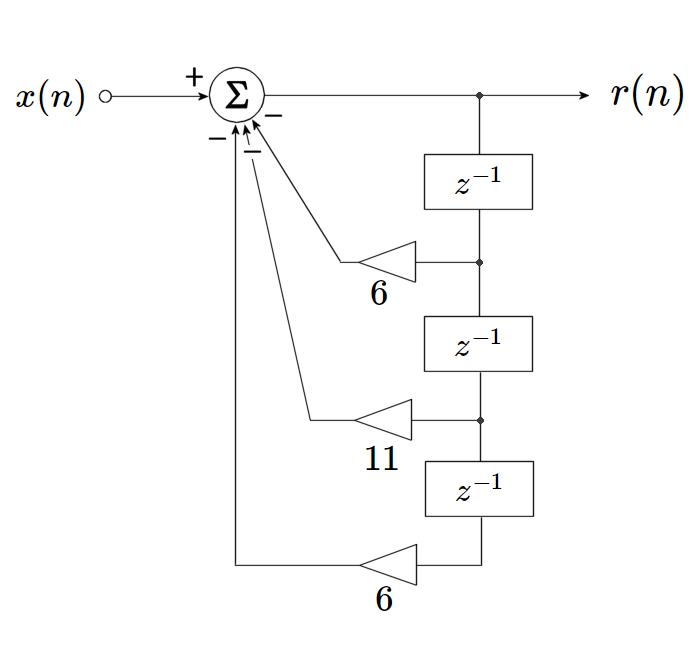
図9 : $x^3+6 x^2+11 x+6=0$ を解く回路
(シフト後に全遅延器を $r(n)$ で割る)

インパルス $x(n)=\delta(n)$ を入力して動かしてみると、次表のようになりました。

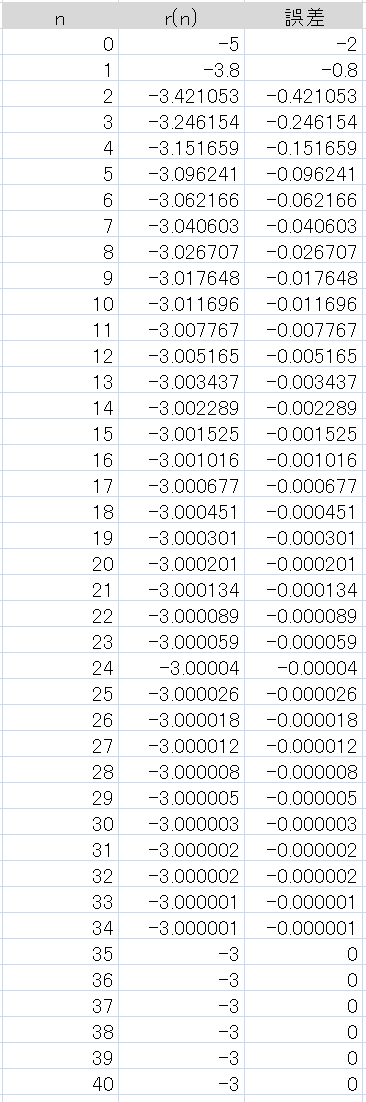
表4 : 図9の回路にインパルスを入れた時の各部の値

うまく絶対値最大の根 -3 に収束しました。

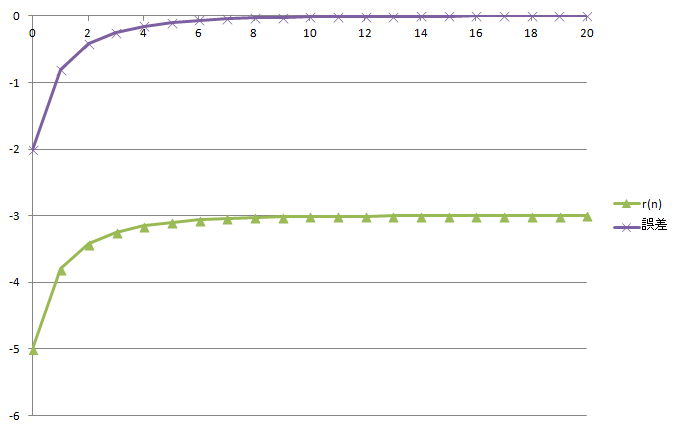
図10 : 表4 のグラフ

例4

同じく図8 の構成で、試しに 10 次の Wilkinson 多項式の絶対値最大根を求めてみましょう。 \begin{eqnarray} F(x) &=& x^{10}-55 x^9+1320 x^8-18150 x^7+157773 x^6-902055 x^5 \nonumber\\ && \quad +3416930 x^4-8409500 x^3+12753576 x^2-10628640 x+3628800 \\ &=& (x-1)(x-2)(x-3)(x-4)(x-5)(x-6)(x-7)(x-8)(x-9)(x-10) = 0 \label{WilkinsonMax} \end{eqnarray} 式(\ref{WilkinsonMax})の因数分解表示から判るように、絶対値最大の根は 10 です。

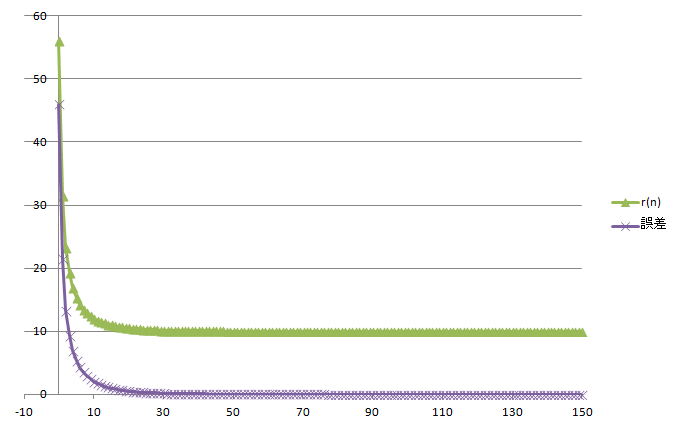
図11 : Wilkinson 多項式 $F(x)=0$ を解かせた時のグラフ

長くなりますので表は掲示しませんが、151 回の反復で 10.000000 になりました。

因数分解

ディジタル・フィルタを使ってこのように絶対値最大の根を見つけ、組立除法で $F(x)$ を $x-\alpha_M$ で割ってゆけば、多項式を実数の範囲で因数分解することもできます。