窓関数の周波数特性

概要

信号に長さ \(L\) の窓関数を掛けた時、どのような周波数特性が信号本来のスペクトルに畳み込まれるのか、いくつかの窓関数について計算しました。

準備

よく使うので、区間 \(\pm\frac{L}{2}\) 内にだけ \(\cos\) 波が \(n\) 周期入っている孤立波形のフーリエ変換を計算しておきます。 \begin{eqnarray} W_n(\omega) &=& \int_{-\frac{L}{2}}^{+\frac{L}{2}} \cos\left(2n\pi\frac{t}{L}\right) e^{-i\omega t}dt \\ &=& \int_{-\frac{L}{2}}^{+\frac{L}{2}} \cos\left(2n\pi\frac{t}{L}\right) \left\{\cos(-\omega t)+i\sin(-\omega t)\right\} dt \\ &=& \int_{-\frac{L}{2}}^{+\frac{L}{2}} \cos\left(2n\pi\frac{t}{L}\right) \left\{\cos(\omega t)-i\sin(\omega t)\right\} dt \\ &=& \int_{-\frac{L}{2}}^{+\frac{L}{2}} \left\{\cos\left(2n\pi\frac{t}{L}\right)\cos(\omega t)-i\cos\left(2n\pi\frac{t}{L}\right)\sin(\omega t)\right\} dt \\ && 第2項は\ t\ に関して奇関数なので \left[-\frac{L}{2}, +\frac{L}{2}\right] 区間で定積分すると\ 0\ になるから \nonumber\\ &=& \int_{-\frac{L}{2}}^{+\frac{L}{2}} \cos\left(2n\pi\frac{t}{L}\right)\cos(\omega t) dt \\ && 被積分関数は\ t\ に関して偶関数なので \nonumber\\ &=& 2 \int_0^{\frac{L}{2}} \cos\left(2n\pi\frac{t}{L}\right) \cos(\omega t) dt \\ &=& \int_0^{\frac{L}{2}} \cos\left(2n\pi\frac{t}{L}-\omega t\right) + \cos\left(2n\pi\frac{t}{L}+\omega t\right) dt \\ &=& \left[\frac{1}{\frac{2n\pi}{L}-\omega}\sin\left(\frac{2n\pi}{L}t-\omega t\right) + \frac{1}{\frac{2n\pi}{L}+\omega}\sin\left(\frac{2n\pi}{L}t+\omega t\right)\right]_0^{\frac{L}{2}} \\ &=& \frac{1}{\frac{2n\pi}{L}-\omega}\sin\left(\frac{2n\pi}{L}\frac{L}{2}-\omega\frac{L}{2}\right) + \frac{1}{\frac{2n\pi}{L}+\omega}\sin\left(\frac{2n\pi}{L}\frac{L}{2}+\omega\frac{L}{2}\right) \\ &=& \frac{L}{2n\pi-L\omega}\sin\left(n\pi-\frac{L\omega}{2}\right) + \frac{L}{2n\pi+L\omega}\sin\left(n\pi+\frac{L\omega}{2}\right) \end{eqnarray} \(n\) が偶数の場合は \(\sin(n\pi-α)=-\sin(α),\ \sin(n\pi+α)=\sin(α)\) ですから \begin{eqnarray} W_n(\omega) &=& -\frac{L}{2n\pi-L\omega}\sin\left(\frac{L\omega}{2}\right) + \frac{L}{2n\pi+L\omega}\sin\left(\frac{L\omega}{2}\right) \\ &=& \left(-\frac{L}{2n\pi-L\omega} + \frac{L}{2n\pi+L\omega}\right)\sin\left(\frac{L\omega}{2}\right) \\ &=& \frac{2 L^2 \omega}{L^2 \omega^2-4 n^2 \pi ^2} \sin\left(\frac{L\omega}{2}\right) \label{even} \end{eqnarray} \(n\) が奇数の場合は \(\sin(n\pi-α)=\sin(α),\ \sin(n\pi+α)=-\sin(α)\) ですから \begin{eqnarray} W_n(\omega) &=& \frac{L}{2n\pi-L\omega}\sin\left(\frac{L\omega}{2}\right) - \frac{L}{2n\pi+L\omega}\sin\left(\frac{L\omega}{2}\right) \\ &=& \left(\frac{L}{2n\pi-L\omega} - \frac{L}{2n\pi+L\omega}\right)\sin\left(\frac{L\omega}{2}\right) \\ &=& -\frac{2 L^2 \omega}{L^2 \omega^2-4 n^2 \pi ^2} \sin\left(\frac{L\omega}{2}\right) \label{odd} \end{eqnarray} 式(\ref{even}), 式(\ref{odd}) を合わせると \begin{eqnarray} W_n(\omega) &=& (-1)^n \frac{2 L^2 \omega}{L^2 \omega^2-4 n^2 \pi ^2} \sin\left(\frac{L\omega}{2}\right) \label{Wn} \end{eqnarray} 実際に計算する場合、このままでは \(L^2 \omega^2-4 n^2 \pi ^2=0\) の時に分母が 0 になってしまいますが、\(0/0\) 型ですので、\(n\) で場合分けしてロピタル (L'Hôpital) の定理を使って極限を計算します。

\(n=0\) の場合は \(\omega=0\) で \begin{eqnarray} W_0(0) &=& \lim_{\omega\to 0}\frac{2}{\omega} \sin\left(\frac{L\omega}{2}\right) \\ &=& \lim_{\omega\to 0} \frac{\frac{d}{d\omega}\left\{2 \sin\left(\frac{L\omega}{2}\right)\right\}}{\frac{d}{d\omega}\omega} \\ &=& \lim_{\omega\to 0} L \cos \left(\frac{L w}{2}\right) \\ &=& L \label{L} \end{eqnarray} \(n=1,2,3,\cdots\) の場合は \(\omega=\displaystyle\frac{2 n \pi}{L}\) で \begin{eqnarray} W_n\left(\frac{2 n \pi}{L}\right) &=& \lim_{\omega\to \frac{2 n \pi}{L}} \frac{\frac{d}{d\omega}\left\{2 (-1)^n L^2 \omega \sin\left(\frac{L\omega}{2}\right)\right\}}{\frac{d}{d\omega}\left\{L^2 \omega^2-4 n^2 \pi^2\right\}} \\ &=& 2 (-1)^n L^2 \lim_{\omega\to \frac{2 n \pi}{L}} \frac{\frac{d}{d\omega}\left\{\omega \sin\left(\frac{L\omega}{2}\right)\right\}}{\frac{d}{d\omega}\left\{L^2 \omega^2\right\}} \\ &=& 2 (-1)^n \lim_{\omega\to \frac{2 n \pi}{L}} \frac{\frac{d}{d\omega}\left\{\omega \sin\left(\frac{L\omega}{2}\right)\right\}}{\frac{d}{d\omega}\omega^2} \\ &=& 2 (-1)^n \lim_{\omega\to \frac{2 n \pi}{L}} \frac{\sin \left(\frac{L \omega}{2}\right)+\frac{1}{2} L \omega \cos \left(\frac{L \omega}{2}\right)}{2w} \\ &=& \frac{(-1)^n L}{2 n\pi}\left\{\sin (n\pi)+n\pi \cos (n\pi)\right\} \\ &=& \frac{(-1)^n L}{2 n\pi} n\pi (-1)^n \\ &=& \frac{L}{2} \label{L2} \end{eqnarray}

矩形窓 (rectangular window)

長さ \(L\) の矩形窓 \begin{eqnarray} w(t) &=& \left\{ \begin{array}{rl} 1, & -\frac{L}{2} \leq t\lt \frac{L}{2} \\ 0, & その他 \end{array} \right. \end{eqnarray}

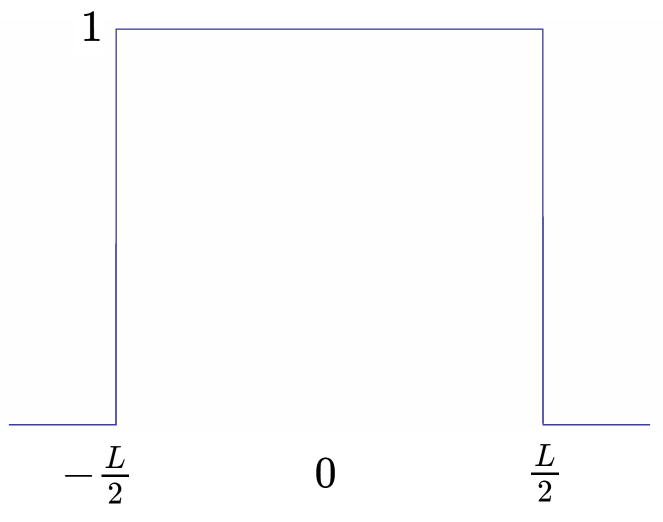
矩形窓

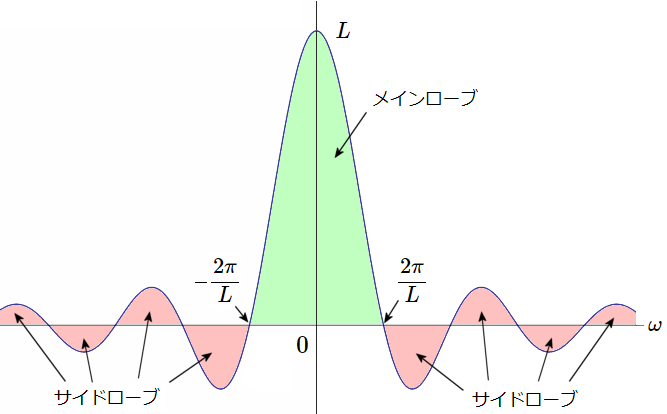
矩形窓の周波数特性

ハン窓 (hann window)

一般に \(a,b\) を定数とする長さ \(L\) の窓 \begin{eqnarray} w(t) &=& \left\{ \begin{array}{rl} a+b\cos(2\pi\frac{t}{L}), & -\frac{L}{2} \leq t\lt \frac{L}{2} \\ 0, & その他 \end{array} \right. \label{Han} \end{eqnarray}

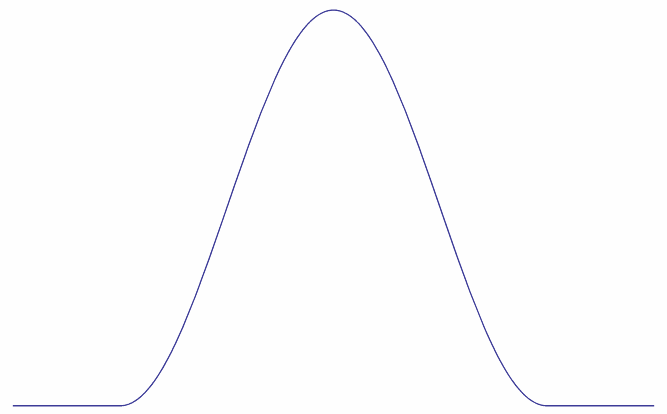
ハン窓

ハン窓は \(a=b=1/2\) としたものですから、その周波数特性は式(\ref{W01})より \begin{eqnarray} W(\omega) &=& \left(\frac{1}{\omega}-\frac{L^2 \omega}{L^2 \omega^2-4 \pi ^2}\right) \sin\left(\frac{L\omega}{2}\right) \\ \end{eqnarray} ただし式(\ref{L}),式(\ref{L2})より \(W_0(0)=L,\ W_1\left(\displaystyle\frac{2 \pi}{L}\right)=\displaystyle\frac{L}{2}\) です (以下、同様)。

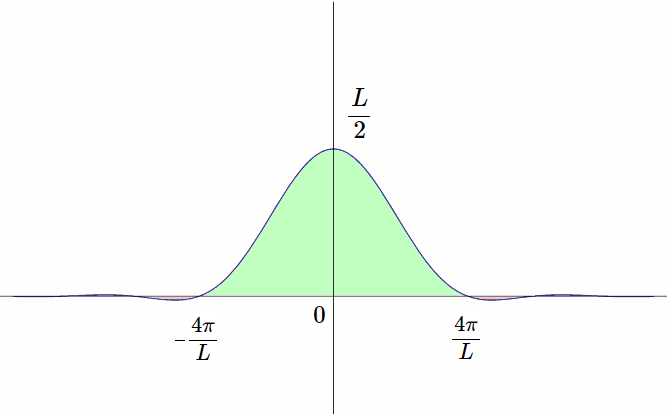
ハン窓の周波数特性

ハミング窓 (hamming window)

ハミング窓は式(\ref{Han})で \(a=0.54, b=0.46\) としたものです。

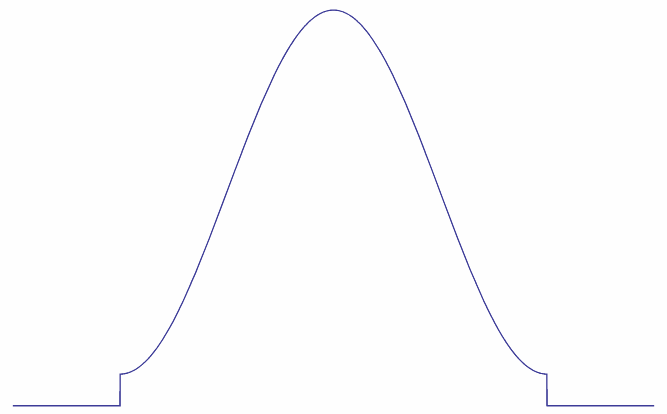
ハミング窓

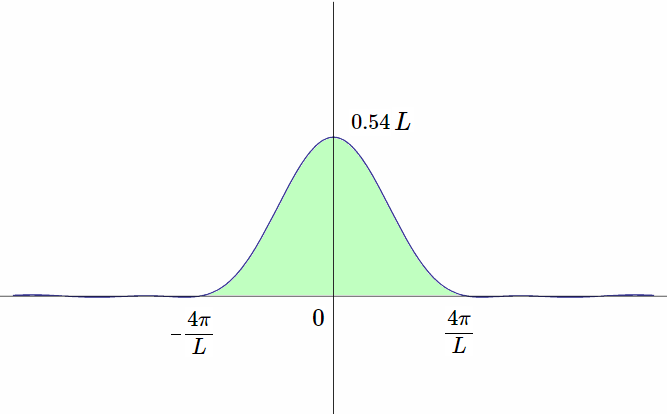
ハミング窓の周波数特性

ブラックマン窓 (Blackman window)

一般に \(a,b,c\) を定数とする長さ \(L\) の窓 \begin{eqnarray} w(t) &=& \left\{ \begin{array}{rl} a+b\cos(2\pi\frac{t}{L})+c\cos(4\pi\frac{t}{L}), & -\frac{L}{2} \leq t\lt \frac{L}{2} \\ 0, & その他 \end{array} \right.\label{abc} \end{eqnarray} の周波数特性は \begin{eqnarray} W(\omega) &=& a W_0(\omega) + b W_1(\omega) + c W_2(\omega) \\ && 式(\ref{Wn}) より \nonumber\\ &=& a \frac{2 L^2 \omega}{L^2 \omega^2} \sin\left(\frac{L\omega}{2}\right) - b \frac{2 L^2 \omega}{L^2 \omega^2-4 \pi ^2} \sin\left(\frac{L\omega}{2}\right) + c \frac{2 L^2 \omega}{L^2 \omega^2-16 \pi ^2} \sin\left(\frac{L\omega}{2}\right) \\ &=& 2\left(a\frac{1}{\omega}-b\frac{L^2 \omega}{L^2 \omega^2-4 \pi ^2}+c \frac{L^2 \omega}{L^2 \omega^2-16 \pi ^2}\right) \sin\left(\frac{L\omega}{2}\right) \label{W012} \end{eqnarray}

ブラックマン窓は式(\ref{abc}) で \(a=0.42, b=0.5, c=0.08\) としたものです。

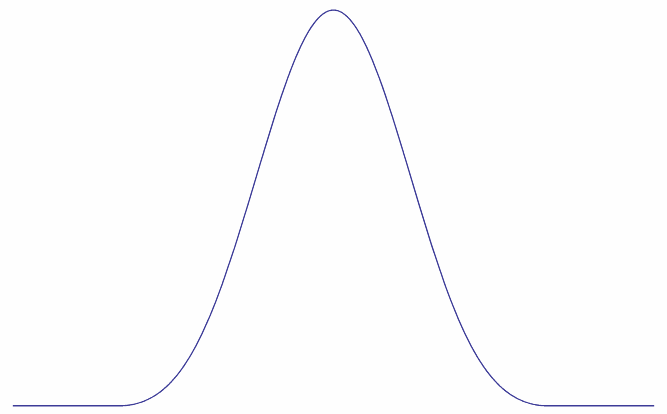
ブラックマン窓

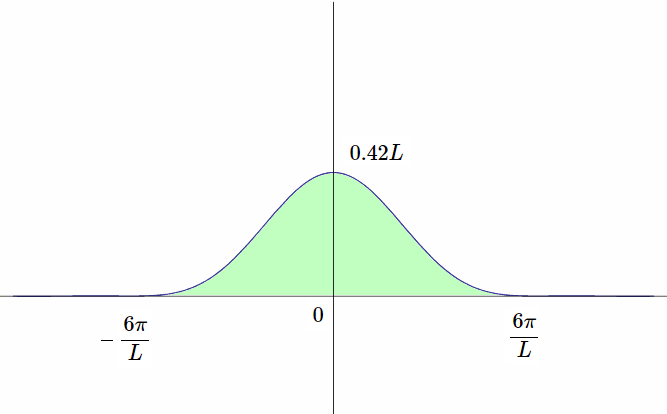
ブラックマン窓の周波数特性

各窓関数の周波数特性を比較する

今回取り上げた 4 つの窓関数の周波数特性を重ね描きすると次のようになります。

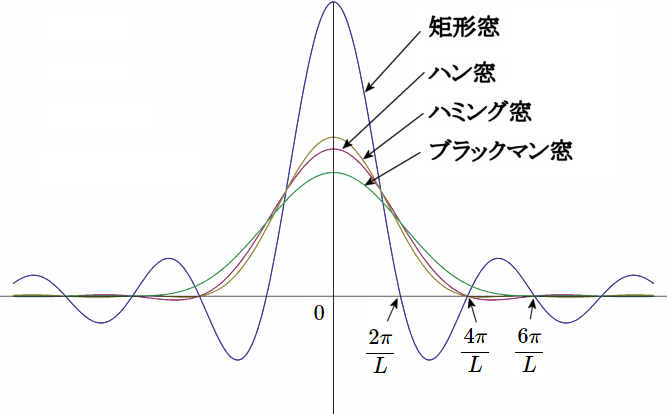
各窓の周波数特性

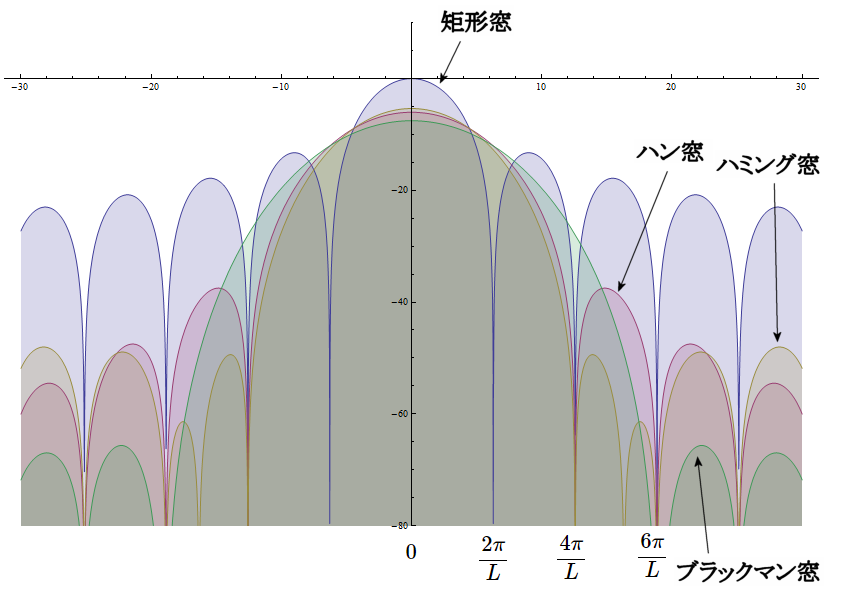
\(L=1\) の場合の各窓の周波数特性を dB で比較
(縦軸の一番下は -80dB)