固定小数点の丸め誤差

固定小数点

数値 \(x\) を固定小数点で \begin{eqnarray} x &\simeq& m\cdot 2^e \end{eqnarray} と近似表現する場合を考えます。ここで \(m\) は \(B\) bit の符号付き整数 \(-2^{B-1}\leq m\lt 2^{B-1}\)、\(e\) はビット・シフト量を表す符号付き整数(負の場合が多い)です。

丸め誤差

ビット長 \(B=3, e=-2\) の場合の固定小数点の「丸め」を、関数としてグラフ化したものを以下に例示します。

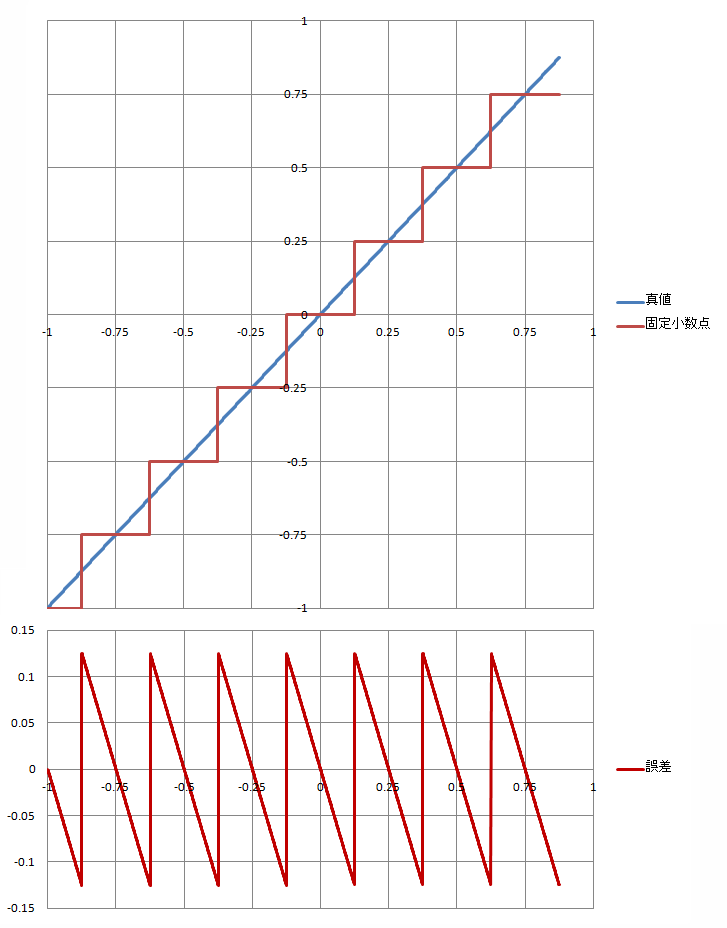
丸め関数と、その誤差
(上段:丸め関数, 下段:誤差)

図から解るように、\(\pm 0.125\) の誤差がノコギリ波状に発生しています。

一般に固定小数点で丸めを行うと \(\pm 2^{e-1}\) の範囲内の誤差を生じます。

固定小数点の量子化幅 (LSB の大きさ) を \begin{eqnarray} \varepsilon=2^e \end{eqnarray} とすると、誤差 \(X\) の生じうる範囲は \(X\in\left[-\frac{1}{2}\varepsilon,+\frac{1}{2}\varepsilon\right)\) で、この範囲内で誤差が等確率に発生する「一様分布」の場合、誤差の期待値(平均)は \begin{eqnarray} \mu &=& 0 \end{eqnarray} この範囲の確率密度関数は \begin{eqnarray} f(X)&=&\displaystyle\frac{1}{\varepsilon} \end{eqnarray} となります。

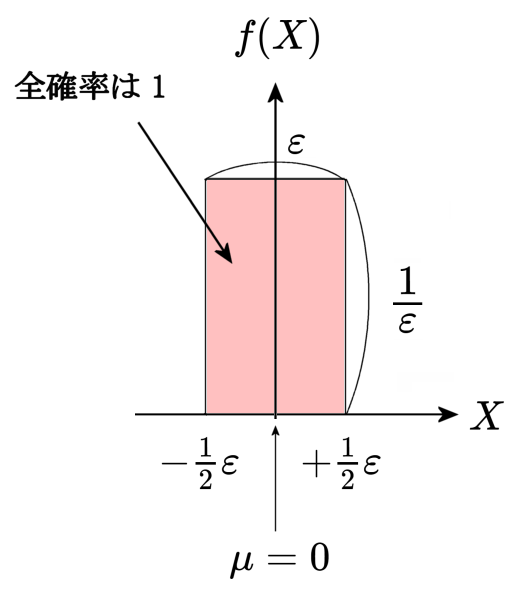
全確率は 1 だから、幅 \(\varepsilon\) で一様分布する誤差の確率密度は \(\displaystyle\frac{1}{\varepsilon}\)

従って、丸めによる誤差パワーの期待値(分散)は \begin{eqnarray} \sigma^2 &=& \int_{-\frac{1}{2}\varepsilon}^{+\frac{1}{2}\varepsilon} f(X) (X-\mu)^2 dX \\ &=& \int_{-\frac{1}{2}\varepsilon}^{+\frac{1}{2}\varepsilon} \frac{1}{\varepsilon} X^2 dX \\ &=& \frac{1}{3\varepsilon}\left[X^3\right]_{-\frac{1}{2}\varepsilon}^{+\frac{1}{2}\varepsilon} \\ &=& \frac{1}{3\varepsilon}\left\{\left(+\frac{1}{2}\varepsilon\right)^3 - \left(-\frac{1}{2}\varepsilon\right)^3\right\} \\ &=& \frac{1}{3\varepsilon} \cdot \frac{2}{8}\varepsilon^3 \\ &=& \frac{1}{12} \varepsilon^2 \end{eqnarray} となります。

応用

信号の振幅が量子化幅 \(\varepsilon\) に比べて十分大きく、かつ十分複雑な(量子化誤差の発生が一様分布とみなせる)場合、丸めによって発生するノイズのパワーを \begin{eqnarray} \sigma^2 &=& \frac{1}{12} \varepsilon^2 \end{eqnarray} で見積もれるという結果は、要求される S/N 比から固定小数点ディジタル・フィルタの演算ビット長を決定する際など、頻繁に使われます。