演算量最小の FFT 畳み込み

本文は2017年11月11日に八戸工業大学で開催された音楽音響研究会(日本音響学会の分科会のひとつ)で発表した内容をまとめたものです。

概要

ストリーム入力に対して複雑で長いインパルス応答を畳み込む場合、FIR でフィルタリングしたのでは演算量が多すぎて、FFT で畳み込む方が速い場合があります。

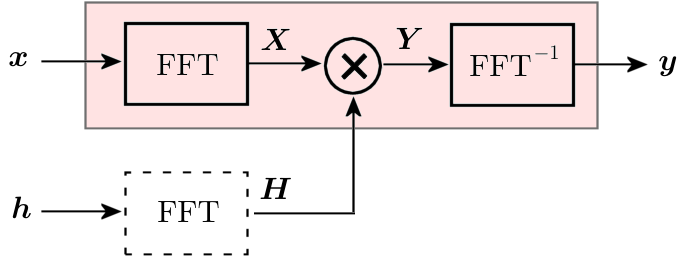
図1 : FFT で畳み込み

レイテンシーの制約がきつくない場合は FFT 点数の選択に自由度がありますが、その中でサンプル当たりの演算量 (CPU/DSP 等の負荷) が最小となる FFT 点数はどれでしょうか?

この問いに答える見積もり公式を導出致しました。

サンプル当たり演算量モデル

N 点 FFT で畳み込みを行う場合、実装には

DC と Nyquist 周波数の虚部は 0 なので、虚部の乗算を省略する
回転子 \(W\) に対して \(W^0=1\) の乗算は省略、\(W^{N/2}=-1\) の乗算は符号反転、\(W^{N/4}=-i,\ W^{3/4N}=i\) の乗算は実部・虚部の入れ替えと符号反転で済ませる
2 つの実数波形を一度に FFT する
基数 2 以外の FFT を使用する
負の周波数は正の周波数のスペクトルの複素共役を利用する

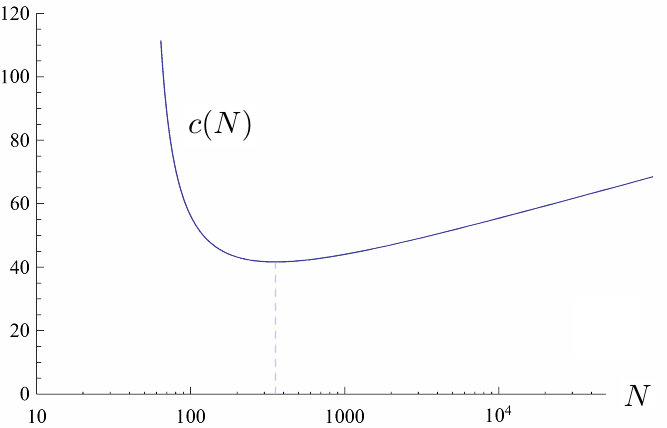
など、高速化のために様々なテクニックを使いますので、これらを統一的に表す畳み込み演算量モデル \begin{eqnarray} C(N) &=& a N\log N + b N + c,\ a\neq 0 \label{CNmodel} \end{eqnarray} を考え、長さ L のインパルス応答を畳み込む際に、入力波形をフレーム分割する長さ M として、線形畳み込みが成立する限界サンプル数 \begin{eqnarray} M &=& N-L+1 \end{eqnarray} を採用すると、サンプル当たり演算量は \begin{eqnarray} c(N) &=& \frac{C(N)}{M}\ =\ \frac{a N\log N + b N + c}{N-L+1} \label{cN} \end{eqnarray} となり、下図のように、ある \(N\) で最小になります。

図2 : c(N) の例
(破線の所でサンプル当たり演算量が最小になる)

演算量の最小解

サンプル当たり演算量 \(c(N)\) が最小になる \(N\) は \begin{eqnarray} \frac{d}{dN}c(N) &=& \frac{d}{dN} \frac{a N\log N + b N + c}{N-L+1} \\ &=& \frac{a N +a(1-L) \log N + a (1-L) +b(1-L)-c}{(N-L+1)^2} \ =\ 0\label{dc0} \end{eqnarray} を解いて、次のように求めることができます。 \begin{eqnarray} N_{opt} &=& (1-L)W_{-1}\left(\frac{1}{1-L}e^{\frac{(a+b)(L-1)+c}{a(1-L)}}\right) \label{Nopt} \end{eqnarray} ここに \(W_{-1}\) は、図 3 に示す Lambert W 関数の下側の分枝です。

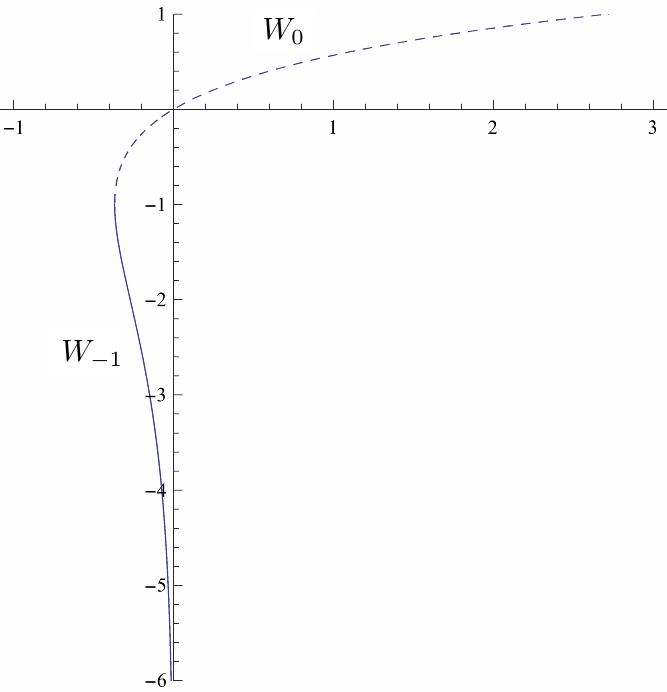
図3 : Lambert W 関数

FFT 点数 \(N\) は基数による制限がありますので、実際には、\(N_{opt}\) に近い \(N\) を採用することになります。

なお、CPU や DSP のようにキャッシュを備えた計算デバイスでは、演算量が同じでも、キャッシュに収まるか否かで計算時間が大幅に違ってきますので、計算時間が問題になる場合はキャッシュの影響を考慮する必要があります。

式(\ref{Nopt})の詳細な導出方法、PC 上でのシミュレーション結果などは音楽音響研究会資料 MA2017-49 をご覧下さい。