ラプラス逆変換の公式を導く
因果的な信号 $f(t)$
\begin{eqnarray}
f(t) &=& 0,\ t<0
\end{eqnarray}
のラプラス変換は、次のように定義されます。
\begin{eqnarray}
F(s) &=& \int_0^\infty f(t) e^{-s t} dt \label{Fs}
\end{eqnarray}
$F(s)$ のラプラス逆変換は次のように計算できます。
\begin{eqnarray}
f(t) &=& \frac{1}{2\pi i} \int_{\sigma-i\infty}^{\sigma+i\infty} F(s) e^{s t} ds \label{invL}
\end{eqnarray}
ただし $\sigma$ は実数で、$F(s)$ の極の実部の最大値より大きく取るものとします。
【参考】この積分路をブロムウィッチ (Bromwich) 積分路といいます。
なぜ式(\ref{invL})で $F(s)$ から元の信号 $f(t)$ が得られるのか、考えてみましょう。
コーシーの積分公式より、正則な領域に含まれる周回積分路 $C$ 内の点 $p$ を考えると、次式が成り立ちます。
\begin{eqnarray}
F(p) &=& \frac{1}{2\pi i}\int_C \frac{F(s)}{s-p} ds
\end{eqnarray}
周回積分路 $C$ として、図1のように、上から下に向かう線分 $B$ と、その右側の半円 $\Gamma$ が合わさったものを採用します。
\begin{eqnarray}
F(p)
&=& \frac{1}{2\pi i} \int_C \frac{F(s)}{s-p} ds \nonumber\\
&=& \frac{1}{2\pi i} \left\{ \int_{B} \frac{F(s)}{s-p} ds + \int_\Gamma \frac{F(s)}{s-p} ds \right\}
\end{eqnarray}
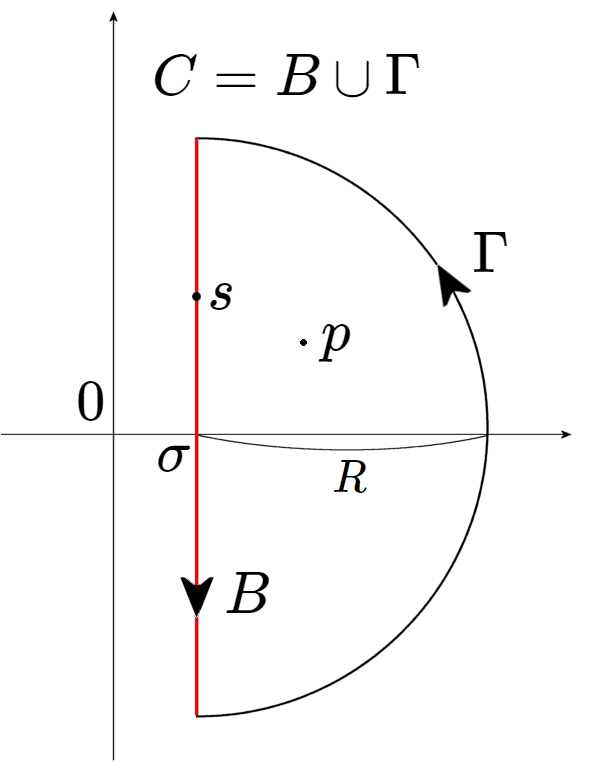図1 : $F(p)$ は $C$ 上の周回積分で計算できる
$F(s)$ が無限遠点で $\displaystyle\lim_{|s|\to\infty} |F(s)|=0$ を満たす場合、$R\to\infty$ で半円 $\Gamma$ 部分の線積分は 0 になりますから、$F(p)$ は次のように書けます。
\begin{eqnarray}
\require{cancel}
F(p)
&=& \frac{1}{2\pi i} \lim_{R\to\infty} \left\{ \int_{B} \frac{F(s)}{s-p} ds + \cancel{\int_\Gamma \frac{F(s)}{s-p} ds} \right\} \\
&=& \frac{1}{2\pi i} \int_{\sigma+i\infty}^{\sigma-i\infty} \frac{F(s)}{s-p} ds \\
&& 線積分の向きを逆にすれば \nonumber\\
&=& -\frac{1}{2\pi i} \int_{\sigma-i\infty}^{\sigma+i\infty} \frac{F(s)}{s-p} ds \label{Fp}
\end{eqnarray}
ここで $\displaystyle\int_0^\infty e^{-(p-s)t} dt$ というものを考えると、$p$ は $C$ の内部にあり $B$ より右にありますから $Re[p-s]>0$ で、
\begin{eqnarray}
\int_0^\infty e^{-(p-s)t} dt
&=& \left[ -\frac{1}{p-s} e^{-(p-s)t} \right]_0^\infty \\
&& Re[p-s]>0\ だから \left.e^{-(p-s)t}\right|_{t=\infty}=0\ であり、\left.e^{-(p-s)t}\right|_{t=0}=1\ なので \nonumber\\
&=& -\frac{1}{p-s} \left\{ 0 - 1\right\} \\
&=& \frac{1}{p-s}
\end{eqnarray}
より、以下が成り立ちます。
\begin{eqnarray}
\frac{1}{s-p} &=& -\int_0^\infty e^{-(p-s)t} dt
\end{eqnarray}
これを式(\ref{Fp})に代入すると、$F(p)$ は次のように書けます。
\begin{eqnarray}
F(p)
&=& \frac{1}{2\pi i}\int_{\sigma-i\infty}^{\sigma+i\infty} F(s) \left[ \int_0^\infty e^{-(p-s)t} dt\right]\ ds \\
&=& \int_0^\infty \left[ \frac{1}{2\pi i} \int_{\sigma-i\infty}^{\sigma+i\infty} F(s) e^{s t} ds \right] e^{-p t} dt \label{Fp1}
\end{eqnarray}
一方、ラプラス変換の定義式(\ref{Fs})の $s$ を $p$ に置き換えると次のようになります。
\begin{eqnarray}
F(p) &=& \int_0^\infty f(t) e^{-p t} dt \label{Fp2}
\end{eqnarray}
式(\ref{Fp1})と式(\ref{Fp2})を見比べると、式(\ref{Fp1})の [ ] の中は式(\ref{invL})そのものであり、それが式(\ref{Fp2})の $f(t)$ に相当することが分かります。
よって、次式でラプラス逆変換して元の信号 $f(t)$ を求めることができます。
\begin{eqnarray}
f(t) &=& \frac{1}{2\pi i} \int_{\sigma-i\infty}^{\sigma+i\infty} F(s) e^{s t} ds \nonumber
\end{eqnarray}